Bored on a Monday
On April 1st of last year, I biked to work to find that a nearby fire had taken out the internet connection to the office. We were pretty much dead in the water without access to Confluence, GitHub, Jira, etc, and my colleague Jake Wood offered to give a lightning talk on a particular mathematical entity -- a space-filling curve known as the "dragon curve."
Physically Generating the Curve
The introduction is as follows: you start with a narrow strip of paper, held up vertically. You fold the top of the strip downwards to meet the bottom. Now there is one fold at the top and there are two loose ends on bottom. You again bring the top down towards the bottom, folding to the right. The image below shows the first three folds. Repeatedly folding a strip of paper.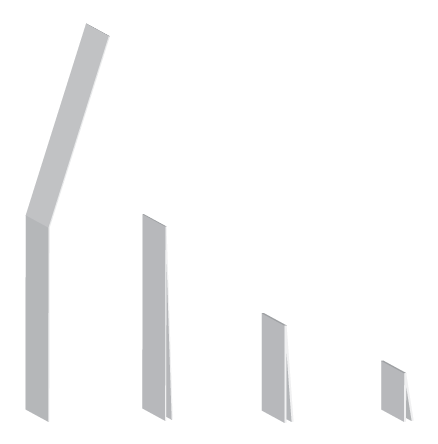
Unfolding the strip and fixing all internal folds at 90 degrees results in the curve shown below. I've drawn in red, green, and blue indicators to show which internal folds are the result of the first, second, and third external folds, respectively.
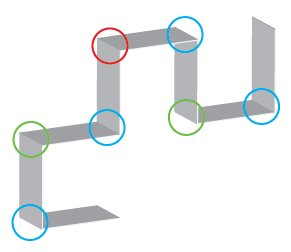
Result of unfolding after the first three folds.
The interesting thing is that, if you continue making folds in this way, you end up with an increasingly complex curve. This curve exhibits some large scale self-similarity, and it has the interesting property that it never crosses itself. Creating the dragon curve using seven consecutive external folds results in the following image. This time around, color has been added to help keep track of the original strip. Adjacent segments are colored similarly.
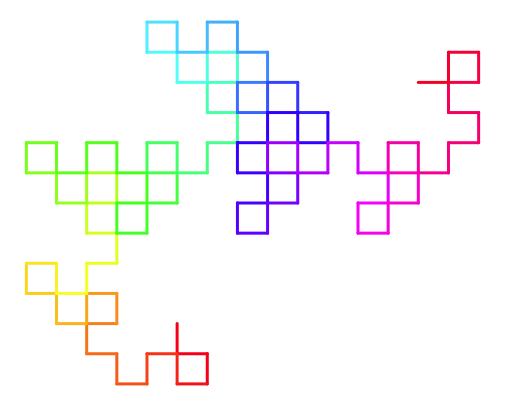
Dragon curve created from seven identical external folds.
Representing and Generating the Structure
Imagine you're an ant walking along the curve. Because the turns are defined to be fixed at 90 degrees, you will only ever have to follow two instructions to trace the path -- take a left or take a right. If we use a \(+1\) to indicate a right turn and \(-1\) to mean a left turn, the sequence to reproduce the simple curve created using three external folds is as follows: \(\{{\color{#47c8ff}+1}, {\color{#2fad2f}+1}, {\color{#47c8ff}-1}, {\color{red}+1}, {\color{#47c8ff}+1},{ \color{#2fad2f}-1}, {\color{#47c8ff}-1}\}\). There are a few things to note here.
- Because our curve-generating algorithm is to always fold the top of the paper strip down and to the right, the first move in the sequence will always be a right turn.
- The \(n\)th external fold will introduce \(2^n\) total folds along the curve. Our first three external folds introduced \({\color{red}2^0}\), \({\color{#2fad2f}2^1}\), and \({\color{#47c8ff}2^2}\) corners in the path.
- Because of the alternating orientation of paper strip, an external fold will always introduce alternating left and right turns. Notice in the sequence above that any color taken on its own alternates back and forth between left and right turns.
With these rules, we have everything we need in order to build the move sequence for the dragon curve. The following algorithm will suffice.
- Start with \(n=0\). Let \(M=\{\}\) be the sequence of moves generating the curve.
- Generate a sequence of \(2^n\) alternating \(1\)'s and \(-1\)'s, starting with \(+1\).
- Riffle (do an alternating shuffle of) this new sequence into \(M\).
- Increment \(n\).
- Go back to step 2.
So from previously, we have \(M=\{{\color{#47c8ff}+1}, {\color{#2fad2f}+1}, {\color{#47c8ff}-1}, {\color{red}+1}, {\color{#47c8ff}+1},{ \color{#2fad2f}-1}, {\color{#47c8ff}-1}\}\) as the sequence up to the 3rd external fold (up to \(n=2\) when 0-indexed). Following the algorithm to add the next external fold, we set \(n=3\), and generate \(2^3\) alternating + and - 1's to get \(\{{\color{#983ab5}+1, -1, +1, -1, +1, -1, +1, -1}\}\), and riffle this into \(M\). Doing this gives
\[M=\{{\color{#983ab5}+1}, {\color{#47c8ff}+1},{\color{#983ab5}-1}, {\color{#2fad2f}+1}, {\color{#983ab5}+1}, {\color{#47c8ff}-1}, {\color{#983ab5}-1}, {\color{red}+1}, {\color{#983ab5}+1}, {\color{#47c8ff}+1}, {\color{#983ab5}-1}, { \color{#2fad2f}-1}, {\color{#983ab5}+1}, {\color{#47c8ff}-1}, {\color{#983ab5}-1}\}.\]
Note that the turns taken for the collective path are by no means alternating. It is only the case that a single external fold introduces alternating internal folds.
Variations on a Theme
If you're anything like me, you're beginning to wonder what happens when some of the folds are not made downward and to the right. If there are five or six external folds, and a couple of these are made to the left instead of to the right, how is the larger curve changed? Will it now be allowed to cross over itself, or will it continue avoiding overlap? Taking a step back, we can imagine an external fold sequence. A sequence of folds could be represented as a binary number, where the leftmost digit is the original fold, the following digit is the following fold, etc. If we choose \(0\) to be a right fold and \(1\) to be a left fold, we conclude that we have only been discussing curves made from \(0\), \(00\), \(000\), \(0000\), \(00000\), etc this whole time.
Adding to our algorithm, a leftward external fold can be generated by riffling in a \(2^n\)-size alternating sequence starting with \(-1\) rather than \(+1\). Here are the curves generated by all permutations of four external folds. I've arbitrarily chosen to orient the curves so that the first segment of the path is walked in the \(-y\) direction.

All variations on four consecutive external folds.
You can see that some of these are unique, while others are just rotations of each other. That should make sense, as \(0000\) and \(1111\), for instance, represent the same physical thing -- 4 folds in the same direction in sequence. Adding more and more folds, you can generate curves whose general shape diverges significantly from the curve made using all folds in one particular direction.

Curve created from ten external folds in the following sequence: 0101011000.
If you'd like to play around with these paths for yourself, or see the code used to create the images in this post, check out the demo on codepen.